Modèles des structures harmoniques

14h30 – 18h30

IRCAM - Salle Stravinsky
Entrée libre dans la mesure des places disponibles

Pour cette dernière séance de la saison, nous opérons un retour sur les fondamentaux avec un thème classique du séminaire MaMuX, revu à la lumière de récentes approches de la modélisation musicale et harmonique à l'aide des outils mathématiques et informatiques.

Programme [PDF]

• 14h30-14h45 : John Mandereau – Introduction de la séance
• 14h45-15h30 : Gilles Baroin et Stéphane de Gérando – Sons et Couleurs en Hyperespace : L’Hypersphère des Spectres
• 15h30-16h15 : Louis Bigo – Différentes utilisations de l'espace pour la modélisation de structures harmoniques

• 16h30-17h15 : François Durand – Coupure enharmonique, complétude et applications
• 17h15-18h : Hugues Seress – La tonalité dans l’œuvre de Bartók entre 1903 et 1918 : Un exemple de conjonction entre distance intervallique, polarité, et orientation modale

Nous présentons ici une évolution des recherches développées initialement par Gilles Baroin : Application de la théorie des Graphes à des objets musicaux et visualisations en hyperespace, et y ajoutons l’expérience de chercheur et de compositeur de Stéphane de Gérando.

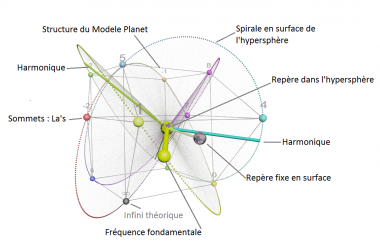
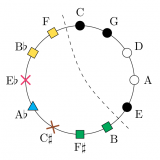
Le modèle « Planet-4D » est une adaptation originale d’un Tonnetz en hyperspace ou chaque classe de hauteur est répartie de façon symétrique en surface d’une hypersphère. Ce modèle fut ensuite étendu à « l’hypersphère des accords » ou le spectateur suit les progressions d’accords parfaits de la musique tonale dans un hyperespace équivalent à l’espace dual du Tonnetz. La dernière évolution, « Hypersphère of AnySet », permet de représenter spatialement n’importe quel agrégat de notes (classes de hauteurs) afin d’analyser l’harmonie d’œuvres musicales tonales ou atonales et d’y déceler des symétries qui seraient pas forcément évidentes avec un mode de représentation habituel.

Dans le cadre de cette présentation de notre recherche, nous considérons l’ensemble du spectre sonore audible et le projetons sur une spirale en surface d’une hypersphère dans un espace à 4 dimensions. Nous obtenons un modèle général continu de représentation visuelle sonore et musicale. Ce modèle est utilisé pour visualiser à la fois des notes, des spectres de sons ou n’importe quel son audible décomposé en fréquences. Le modèle est en cours de développement, nous montrerons les premiers résultats des expériences. Nous nous interrogerons sur la potentialité esthétique et artistique de ce modèle, notamment dans le cadre d’une création artistique liant paramètres sonores et visuels.

Les vidéos seront disponibles sur le site MatheMusic4D.

Cet exposé présente différentes manières d'utiliser l'espace pour la visualisation et l'analyse de structures harmoniques. Notre approche est motivée par la recherche d'espaces symboliques faisant émerger la singularité d'une séquence musicale qui y est représentée. Cette motivation se situe au coeur du calcul spatial que nous appliquons à l'aide du langage dédié MGS. Après avoir présenté rapidement ce langage, nous proposerons deux types d'espace de hauteurs pour représenter les structures harmoniques : Des espaces irréguliers, sous forme de complexes simpliciaux résultant d'un calcul, représentent eux-même les structures harmoniques. Puis des réseaux de notes réguliers (plus connus sous le nom de Tonnetz) que nous voyons comme des espaces construit à priori comme support pour la représentation de structures harmoniques.

Nous adoptons l'hypothèse que, même en tempérament égal, la notation basée sur sept noms de note et des altérations n'est pas purement arbitraire mais révèle des propriétés musicales plus profondes. Afin de l'exploiter, nous définissons la coupure enharmonique, un mécanisme qui permet de déterminer l'orthographe enharmonique canonique d'un ensemble de notes. Puis nous définissons les ensembles complets, des paradigmes sonores dont dérivent toutes les gammes et tous les accords.

Les applications présentées couvrent plusieurs domaines de l'harmonie :

• dégager des gammes et des accords remarquables ainsi que leurs interconnexions,
• catégoriser les sonorités des douze notes du tempérament dans le champ harmonique généré par un accord,
• proposer une nouvelle approche des accords, non fondée sur les empilements de tierces,
• analyser automatiquement la tonalité et les modulations d'une œuvre.

Un aperçu en images est disponible [ici].

Voir aussi :

• Le texte complet
• …et ses annexes.

Les théories transformationnelles considèrent l’enchaînement des événements harmoniques, accords et tonalités, comme des manipulations exercées sur des catégories, dont résulteraient d’autres catégories. Particulièrement adaptées à la description des unités du discours héritées du système tonal, mais dont la hiérarchie et la fonction auraient été déplacées ou affaiblies, les théories néo-riemanniennes concentrent l’essentiel de leur attention sur la distance d’intervalle. Cependant, cette distance pourrait bien dépendre en partie de la direction dans laquelle s’opèrent les transformations. À l’inverse, si les théories vectorielles prennent en compte le sens de ces transformations, c'est toutefois sans distinction de la classe d'intervalle et de l'orientation modale. Or, on peut raisonnablement penser que, dans la musique de la post-tonalité, le mode d'une catégorie résultant d'une opération, est probablement lié à la nature même de cette opération.

C'est pourquoi, le modèle théorique présenté dans la première partie de cet exposé, proposera de décrire la "tonalité" comme la conjonction entre distance intervallique, polarité et orientation modale des progressions harmoniques. La tonalité de la première modernité (1880-1920) constituant un lieu d'observation privilégié pour mettre à jour l'interaction des trois déclinaisons du phénomène transformationnel, la seconde partie de cet exposé proposera d’appliquer le modèle théorique sur les parcours triadiques de deux extraits d’œuvres de jeunesse de Béla Bartók, aussi différentes que le Quintette avec piano BB33 (1903), d’écriture postromantique, et les Quinze chants paysans hongrois BB79 (1918), empruntant au répertoire paysan.