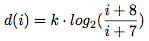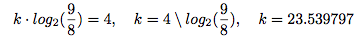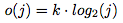James Tenney's Spectral CANON For CONLON Nancarrow

The Spectral CANON For CONLON Nancarrow¹⁾ is a piece for player piano by James Tenney based on the idea of a correspondence between duration and pitch interval ratios. It alludes to Henry Cowell’s invention the rhythmicon or rather his idea of corresponding rhythm, mettre and tempo with harmonic proportions, also influential for its dedicatee, renowned composer Conlon Nancarrow.

Fig. 1 Detail of a schematic 2D visualization showing the pitches and onsets from one of the numberless possible variations of the Spectral CANON for COLON Nancarrow.

This piece dates back from 1974. It has been "extended" by composer Clarence Barlow in 1990 and Irish composer Ciarán Maher created other variations based on Tenney instructions. Important analysis about the work have been published. ²⁾

The piece begins with a low sustained tone which is repeated at a smoothly accelerating pace. Higher tones arrives one after another subdividing the attacks of the first voice. As the piece continues to accelerate and new higher tones appears, complex polyrhythms emerges from the texture until it reaches a state of fusion where one can barely distinguish isolated tones or attacks. The piece concludes with a startling point of total synchronism.

Its concept is quite straightforward. The piece consists of a 24 voices canon. Conventionally, a canon presents more than one of the following features :

1. each voice does not start at the same time but one after another at a fixed time interval
2. each following voice transposes the melody of the first³⁾
3. each voice share the same "rhythm".

However, Tenney's piece is not an ordinary canon, it shows a special approach to that three characteristics. Firstly, the starting times of each following voice 'always' happens after a fixed number of attacks (onsets) of the first voice, instead of a fixed duration. Secondly, the voices doesn't share a proper melody as they play repeatedly just one single tone. Lastly, the voices share not exactly a rhythm but rather a "series of decreasing durations".

We will see each of these aspects below in the next sections. Before, I am going to start with the correspondence between frequencies and durations.

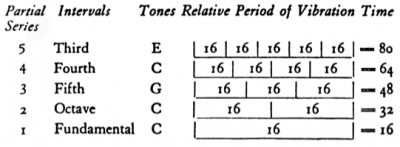
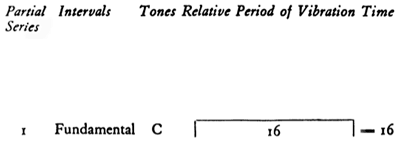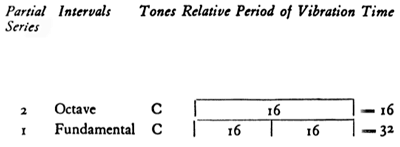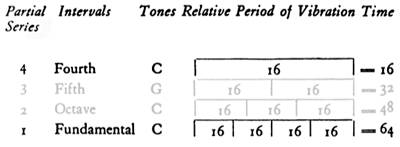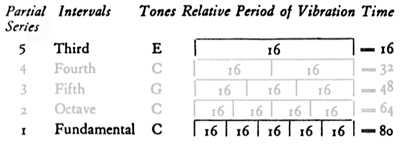
The key to understand the canonic construction and its uniqueness rely in one idea presented in the influential book New Musical Resources (1930) by Henry Cowell. It consists in a way to correspond durations and frequencies where each element in a series of partials multiplies the frequency and the number of rhythmic beats of a given fundamental. In the instance showed by Fig. 2, the second partial of a fundamental 16 Hz plays twice its frequency and its beats, the third partial thrice and so forth. It can also be viewed as an illustration of the mechanism behind the Rhythmicon, a keyboard instrument capable of playing rhythmic ratios with corresponding pitches.

Fig. 2 reproduced from Henry Cowell's New Musical Resources (1930, p.47). It proposes a model to correspond frequency and durations based in the harmonic series.

Cowell called the rhythmic harmony the selection and superposition of durational ratios in an analogy to the construction of chords based in the harmonic series. The C major chord can be formed from the third, fourth and fifth overtones represented as 5:4:3. He proposed that the same proportion could be rendered as a rhythm. In the next audio example we can hear that analogous rhythm of the C major chord played by non-pitched metal percussion. In the example, each cycle of five, four and three beats is played thrice. Each cycle lasts two seconds:

Now, in the example below we have the chord C Major and its rhythm analogy played by a piano. Again, each cycle is played thrice and lasts two seconds:

An instance of this procedure based on a fundamental of 55 Hz and with 24 partials for a duration of four seconds gives us a sonic result very recognizable toward the end of Tenney's Canon:

This would correspond to a Rhythmicon constructed with 24 keys with all them depressed at the same time. Note that we can hear two symmetrical glissandi, descending and then ascending, as a sonic representation of a parabola which can be already glimpsed in the picture above. The same example played twice slower can make it more pronounced:

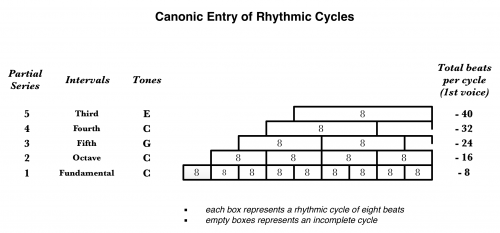
One artifice give us a clue about another important concept in Tenney's piece. By inverting the rhythmic relationships (showed in Fig. 2), while maintaining the frequency ones, it lead us to the basic construct of the canon.

In that case, in contrast to the original procedure, each element in a series of partials multiplies the frequency but divides the number of rhythmic beats of a given fundamental.

[…] On such a keyboard [of a mechanical instrument capable of executing rhythmic ratios] one might make variations, such as playing a rhythmic chord as an arpeggio, which would result result in starting the rhythmical units canonically.

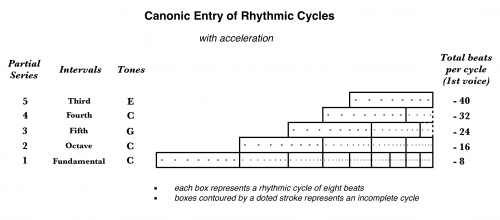
The series of durations was conceived as to produce an exceptionally natural acceleration. (That would be no problem for a human player, but Tenney was writing for a mechanical instrument where each musical event should be precisely fixed in a roll. ) As the then lonely low, first voice begins, it should go faster unaffectedly and almost unperceived while the following voices enter at an equally balanced coordination. That being the case, the question was which kind of acceleration to use.

The perfect form of that acceleration wouldn't be that of an arithmetic neither a geometric progression., where an initial duration is to be decreased by a fixed value or a fixed divisor. Something smoother would be preferred like logarithmic curves.

The series of durations is obtained multiplying the binary logarithm of a sequence of decreasing Superparticular numbers by a constant k:

The denominator of the first superparticular number specifies how many attacks the first voice will play until the second one begins. By inverting the terms of the equation, k allows to specify the first duration in the series.

For the values Tenney used, we have:

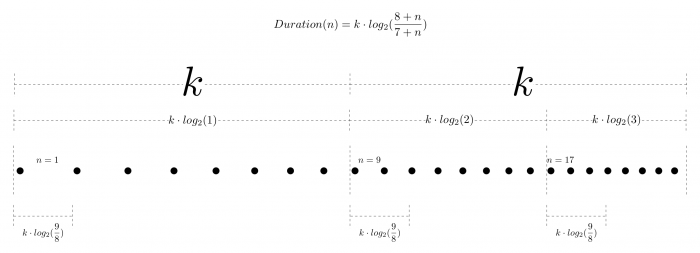
This means that the first duration is four seconds and each voice enters after each eight attacks of the first one. The length of the series is related to the number of voices: when the last (24th) voice enters, the first one plays exactly its last (186th) attack. ⁴⁾

The entry time (or “offset”) for voice v_j in the canon is given by the formula:

For the first voice, the starting time equals k, so the value of k specifies yet how many seconds it will take for the second voice enter.

Hence, the entries of the voices progressively become closer to each other producing a “harmonic” relationship between the different superimposed rhythmic layers: a voice v_j enters when the current duration in voice v₁ is j times the initial duration d(1).

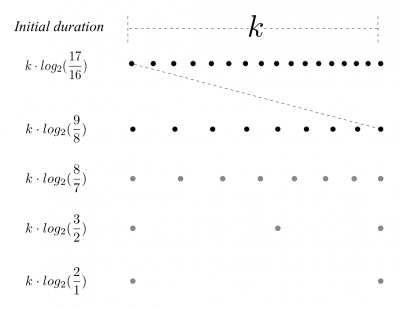
In the original version of the canon, Tenney chose, as is the case in many musical canons, to stop the piece at a point of synchronism where all the voices are still playing, instead to having each one playing until the end, and the last one finishing alone. In order to extend the voices after the end of the series, and keep the early ones playing with the “newer” ones, the series retrograde is systematically appended to the different voices, as in a form of palindrome.

It is worthy of note that the first voice finishes, and therefore starts its retrogradation, precisely when the 24th voice enters. The original version of the piece therefore ends when the first voice completes its palindrome and when the 24th ends its regular series, which is, as we indicated, a point of synchronism (the retrograde of voice 1 and the regular series of voice 24 have the same duration).

In contrast, Barlow’s extended version of the canon continues until the last voice finishes the palindrome. While palindromes or retrogradations are other well-known features of the canons, interestingly here (and especially in Barlow’s version), the end doesn’t sounds at all like a symmetry of the beginning. Indeed, since each voice starts its retrogradation and consequently decelerates at different moments, new unexpected textures emerge, forming melodic patterns, “harmonic glissandi” and harmonic chords due to the occasional points of synchronism.

In order to accomplish a correspondence between pitch and rhythm domains, each voice plays repeatedly one single tone corresponding to its position in the canon, hence reproducing the rhythmic relationship in the frequency domain: voice 2 plays 2 times the frequency of voice 1 (octave), voice 3 plays 3 times the frequency of 1 (fifth), etc. In this way, this piece is also a melodic canon (even if a very elementary one) where each voice plays a transposition of the first one at a precise interval, starting with the traditional ones (transposition at the octave, fifth) and going up to the most unusual ones such as 24/23 or 23/22 (intervals smaller than one semitone).

Our present work mostly takes place in the OpenMusic computer-aided composition environment. OpenMusic is a visual programming language allowing to define and connect together functions and data structures in graphical programs, and to evaluate these programs to produce and transform musical data. From Eq. 1 we can easily implement a function in OpenMusic generating the durations for one voice of the canon. We can also generalize Eq. 2 so as to determine k for any chosen value of the first duration: k = d(1)/log2(9/8). The “palindrome” process is also implemented by simply reversing the resulting series and append the original with the reverse lists of durations. This whole process is illustrated in Figure 1. Figure 2 shows the computation of the voices’ offset times and of the pitches via the implementation of Eq. 3, and using an harmonic series generator for the pitches.

Starting from these implementation of the canon’s generative process, we build a global model allowing to generate the piece, and proposing a number of parameter identified in the previous sections: first duration of the series, pitch fundamental, number of voices, number of elements in the series, application (or not) of the “palidrome”, etc. (see Figure 3). These parameters (and others to be described in the next sections) will allow us to control and generate the score instances. With Tenney’s original parameters, we obtain the score in Figure 4.