Example #1: Alto Saxophone Multiphonics
INTRODUCTION
This example illustrates how audio clustering can be used to quickly structure music by using a simple graph search algorithm. In the following case, the idea is to agglomerate similar sounds together (saxophone multiphonics), based on their harmonic content (superVP masking effects), in order to define the space they occupy (clusters-space network) and to explore/sequence it under specific constraints (shortest Hamiltonian path). By analogy to tonal music, it is to use some sort of a voice leading technique applied to audio signal…
PARAMETERS
Here are the parameters used to generate the following example.
Analysis parameters
- ResampleTo = 44100 Hz
- NormalizeSignal = 1
- WindowType = blackman
- MaxFrequency = 22050 Hz
- FFTPadding = 1
- WindowSize = 200 ms
- HopSize = 100 ms
Clustering parameters
- Clustering type: neat
- Distance type(s): mahalanobis
- Audio feature(s): superVP masking effects ('perceptual' partial tracking)
- Pitch scale: midi notes (linear scale)/quarter-tones (precision)
- Temporal modelling: none
- HMM probability model: neutral
N.B. Refer to the RAW CLUSTERING section below for consulting each clusters and their corresponding sounds separately.
GRAPHS
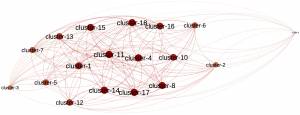
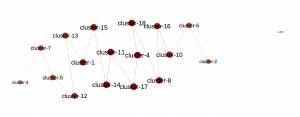
Here is a graphic representation of the resulting clusters space network (MultiDimensional Scaling) and its minimum spanning tree (Kruskal).
These two helps visualising the relationship between the different clusters of sounds (left graph) and how they could be sequenced (right graph)…
N.B. For both graphs, nodes sizes and colours = average weighted degree; larger and darker = high degree, and vice versa…
N.B. This information is also an indicator of centrality/eccentricity of each component in the graph; the more central = the more common, and vice versa…
N.B. These graphs are just representations, not mathematical structures!
SHORTEST HAMILTONIAN PATH (using a Nearest Neighbour algorithm)
Here are two examples of structuring music using a graph search algorithm. The first one explores the previous clusters space network based on the shortest Hamiltonian path principles, meaning that the following sequence of clusters (path) is the one with the minimum total distance that visits each cluster exactly once. In other words, the clusters are sequenced in a way that the global similarity is maximised. The second one uses the exact same principles but instead of being based on the clusters space, it is based on the features space, meaning that each component of the sequence is a unique sound as opposed to a group of sounds.
1) Using the demo standalone,
- the sounds are sequenced according to different Markov chains deduced from each local MST (intra-cluster) while the clusters are sequenced according to the following shortest Hamiltonian path (inter-cluster) calculated using a customised nearest neighbour algorithm. Note that the path below corresponds to the minimum spanning tree above if you read it from right to left.
- Clusters sequence: {9, 2, 6, 10, 16, 8, 18, 4, 17, 11, 14, 15, 1, 13, 12, 5, 7, 3}
- For the clarity of the example, each cluster is triggered every 20 seconds…
2) Still using the demo standalone,
- the sounds are sequenced individually according to the following shortest Hamiltonian path (no clustering beforehand).
- Sounds sequence: {38, 4, 39, 18, 13, 7, 21, 6, 25, 46, 24, 23, 1, 26, 28, 31, 47, 40, 29, 22, 42, 10, 43, 27, 41, 8, 44, 5, 19, 45, 14, 35, 17, 12, 20, 33, 30, 32, 16, 37, 3, 9, 2, 11, 36, 34, 15}
- For the clarity of the example, each sound is triggered every 10 seconds…
N.B. For more information on using a similar approach in the field of instrumental music (music notation), refer to:
- G. Assayag, M. Castellengo, and C. Malherbel, "Functional integration of complex instrumental sounds in music writing", Proceedings of the ICMC, 1985.
N.B. For more information on using a similar approach in the field of sound synthesis/hybridization, refer to:
- C. E. Cella, J. J. Burred, "Advanced sound hybridizations by means of the theory of sound-types", Proceedings of the ICMC, 2013.
RAW CLUSTERING
Here are each of the individual sounds used in the previous examples regrouped under their corresponding clusters so you can hear them individually and compare them ad libitum…
Cluster-1
Cluster-2
Cluster-3
Cluster-4
Cluster-5
Cluster-6
Cluster-7
Cluster-8
Cluster-9
Cluster-10
Cluster-11
Cluster-12
Cluster-13
Cluster-14
Cluster-15
Cluster-16
Cluster-17
Cluster-18