Analyse Formelle des Concepts et Structures Conceptuelles en Musique

Dans le cadre de mon séjour en tant que chercheur invité à l'Institut für Algebra de la Technische Universität Dresden, je m’intéresse à l’application de l’Analyse Formelle des Concepts et des Structures Conceptuelles à la musique. Ce projet de recherche vise à étudier la pertinence des structures d’ordres et des treillis de Galois dans la formalisation de plusieurs problèmes « mathémusicaux », à partir du problème de la classification paradigmatique des structures musicales.

Cette recherche est menée en collaboration avec le groupe de mathématiciens du département d’algèbre travaillant sur la Mathematische Musiktheorie et ses applications en informatique musicale via le logiciel MUTABOR (en particulier Bernhard Ganter, Stefan E. Schmidt, Tobias Schlemmer et Immanuel Albrecht) et Thomas Noll (ESMuC, Barcelona).

Bibliographie

G. Birkhoff, Lattice theory, American Mathematical Society Colloquium Publications, 25 (3rd ed.), Providence, R.I.: American Mathematical Society, 1979 (or. 1940)

W. Reckziegel, “Musikanalyse und Wissenschaft.” Studia Musicologica 9(1-2), 1967, 163-186 (pdf)

M. Barbut, L. Frey, “Techniques ordinales en analyse des données,” Méthodes Mathématiques des Sciences de l’Homme, tome I, Algèbre et Combinatoire, Hachette Universite, 1971.

R. Wille, “Mathematik und Musiktheorie.” In: Schnitzler, G. (Hrsg.): Musik und Zahl. Verlag für systematische Musikwissenschaft, Bonn-Bad Godesberg, 1976, 233-264.

A. R. Bazelow and F. Brickle, “A Partition Problem Posed by Milton Babbitt (Part I)”, Perspectives of New Music, Vol. 14, No. 2, Sounds and Words. A Critical Celebration of Milton Babbitt at 60 (Spring - Summer, 1976), 280-293.

D. Lewin, “On Partial Ordering.” Perspectives of New Music 14/2-15/1, 1976, 252-259.

D. Halsey and E. Hewitt, “Eine gruppentheoretische Methode in der. Musik-theorie,” Jahresber. der Dt. Math.-Vereinigung 80, 150-207, 1978.

D. Starr & Morris, “A general theory of combinatoriality and the aggregate (in two parts),” Perspectives of New Music, 1978

D. Starr, “Sets, Invariance and Partition,” Journal of Music Theory, 1978

D. Lewin, “A Communication on Some Combinatorial Problems”, Perspectives of New Music, 1978

A. R. Bazelow, F. Brickle, “A combinatorial problem in music theory : Babbitt's partition problem (1)”, New York Academy of Sciences, 1979.

R. Wille, “Mathematische Sprache in der Musiktheorie.” In: B. Fuchssteiner, U. Kulisch, D. Laugwitz, R. Liedl (Hrsg.): Jahrbuch Überblicke Mathematik. B.I.-Wissenschaftsverlag, Mannheim, 1980, 167-184.

R. Wille, “Symmetrien in der Musik - für ein Zusammenspiel von Musik und Mathematik,” Neue Zeitschrift für Musik, 1982, 143

R. Wille, “Restructuring lattice theory: an approach based on hierarchies of concepts.” In: I. Rival (ed.): Ordered sets. Reidel, Dordrecht-Boston 1982, 445-470.

R. Wille, “Zur Ordnung von Zeit und Raum - eine Untersuchung im Rahmen der formalen Begriffsanalyse,” 1983

R. Wille, “Sur la fusion des contextes individuals,” Mathématiques et sciences humaines, tome 85, 1984

R. Wille, “Line Diagrams of Hierarchical Concept Systems,” International Classification, 11(2), 1984, 77-86

R. Wille, “Musiktheorie und Mathematik.” In: Götze, H., Wille, R. (Hrsg.): Musik und Mathematik - Salzburger Musikgespräch 1984 unter Vorsitz von Herbert von Karajan, Springer, Heidelberg, 1985, 4-31.

J-L Guigues, V Duquenne, “Familles minimales d'implications informatives resultant d'un tableau de données binaries”, Math. Sci. Humaines 95, 1986

W. O’Connel, “Tone spaces,” Die Reihe, 8, 1986, 35-67.

J. Bennighof, “Set-Class Aggregate Structuring, Graph Theory, and Some Compositional Strategies.” Journal of Music Theory, 31(1), 1987, 51-98.

D. Vuza, “Sur le Rythme Périodique”, Musikometrika I, M. G. Boroda (ed.), Bochum, 1988, 83-126.

K. E. Wolff, “Einführung in die Formale Begriffsanalyse.” In: Actes 19e Séminaire Lotharingien de Combinatoire Strasbourg: Publication de l'Institut de Recherche Mathématique Avancée, 1988, 85-96.

W. Neumaier, Wille, R., “Extensionale Standardsprache in der Musiktheorie – eine Schnittstelle zwischen Musik und Informatik.” In: Hesse, H.P. (ed.) Mikrotöne III: Bericht über das 3. Internationale Symposium “Mikrotonforschung, Musik mit Mikrotönen, Ekmelische Musik”, 28-30 April 1989 in Salzburg, Veröffentlichungen der Gesellschaft für Ekmelische Musik, 6, Helbling, Innsbruck, 1990, 149-167.

R. Wille, “Symmetrie – Versuch einer Begriffsbestimmung.” In K.H. Hofman, R. Wille (eds.), Symmetry of Discrete Mathematical Structures and Their Symmetry Groups. A Collection of Essays, Research and Exposition in Mathematics, Vol. 15, Heldermann Verlag Berlin, 1991, 119-150.

R. Wille, “Begriffsdenken: Von der griechischen Philosophie bis zur Künstlichen Intelligenz heute,” Preprint 1724, 1995.

R. Wille, “Restructuring Mathematical Logic: An Approach Based on Peirce’s Pragmatism.” In Ursini, Aldo and Agliano, Paolo (eds), Logic and algebra, Marcel Dekker, 1996, 267-281

F. Lehmann, Wille R., “A triadic approach to formal concept analysis.” Lecture Notes in Computer Science 954, 1995, 32–43.

R. Wille, “The basic theorem of triadic concept analysis,” Order 12, 1995, 149-158.

B. Ganter and R. Wille, “Applied Lattice Theory: Formal Concept Analysis”, In General Lattice Theory, G. Grätzer (ed.), Birkhäuser, 1997 (ps)

R. D. Morris, “K, Kh, and Beyond.” In Baker J, Beach D, and Bernard J: Music Theory in Concept and Practice. Eastman Studies in Music, University of Rochester Press, 1997, 275-306 (Cf. ToM, p. 384)

Th. Noll, Morphologische Grundlagen der abendländischen Harmonik. In: Moisei Boroda (ed.), Musikometrika 7, Bochum: Brockmeyer, 1997

Th. Noll, “Harmonische Morpheme”, Musikometrika 8, 1998, 7-32.

R. Wille, “Conceptual graphs and formal concept analysis.” In Dickson Lukose, Harry Delugach, Mary Keeler, Leroy Searle, John Sowa (eds), Conceptual Structures: Fulfilling Peirce's Dream, Fifth International Conference on Conceptual Structures, ICCS'97 Seattle, Washington, USA.
It is shown how Conceptual Graphs and Formal Concept Analysis may be combined to obtain a formalization of Elementary Logic which is useful for knowledge representation and processing. For this, a translation of conceptual graphs to formal contexts and concept lattices is described through an example. Using a suitable mathematization of conceptual graphs, basics of a unified mathematical theory for Elementary Logic are proposed.

R. Wille, “Triadic Concept Graphs.” In M.-L. Mugnier, Michel Chein, Conceptual Structures: Theory, Tools and Applications, Springer, ICCS’98, Montpellier, 1998, 194-208
In the paper “Conceptual Graphs and Formal Concept Analysis”, the author has presented a first attempt in unifying the Theory of Conceptual Graphs and Formal Concept Analysis. This context-based approach, which is philosophically supported by Peirce's pragmatic epistemology, is grounded on families of related formal contexts whose formal concepts allow a mathematical representation of the concepts and relations of conceptual graphs. Such representation of a conceptual graph is called a “concept graph” of the context family from which it is derived. In this paper the theory of concept graphs is extended to allow a mathematical representation of nested conceptual graphs by “triadic concept graphs”. As in the preceding paper, our focuss lies on the mathematical structure theory, which later could be used for extending the already developed logical theory of simple concept graphs. The overall aim of this research is to contribute to the development of a contextual logic as basis of Conceptual Knowledge Processing.

B. Ganter, R., Wille, Formal Concept Analysis: Mathematical Foundations, Springer, Berlin, 1999.

R. Kurth, “Partition Lattices in Twelve-Tone Music: An Introduction,” Journal of Music Theory 43(1), 1999, 21-82.

R. Wille, “Contextual Logic summary.” In: G. Stumme (ed.): Working with Conceptual Structures. Contributions to ICCS 2000, Shaker, Aachen 2000, 265-276.

R. Wille, “Eulers Speculum Musicum und das Instrument MUTABOR.” DMV-Mitteilungen, Heft 4/2000, 9-12.

J.F. Sowa, Knowledge representation: logical, philosophical, and computational foundations, Computer Science Series, Brooks/Cole, 2000

R.D. Morris, Class Notes for Advanced Atonal Music Theory (Lebanon, N.H.: Frog Peak Music, 2001).

B.A. Davey, H.A. Priestley, Introduction to Lattices and Order, Cambridge University Press, 2002
Ordered structures have been increasingly recognized in recent years due to an explosion of interest in theoretical computer science and all areas of discrete mathematics. This book covers areas such as ordered sets and lattices. A key feature of ordered sets, one which is emphasized in the text, is that they can be represented pictorially. Lattices are also considered as algebraic structures and hence a purely algebraic study is used to reinforce the ideas of homomorphisms and of ideals encountered in group theory and ring theory. Exposure to elementary abstract algebra and the rotation of set theory are the only prerequisites for this text. For the new edition, much has been rewritten or expanded and new exercises have been added.

G. Stumme, “Formal Concept Analysis on Its Way from Mathematics to Computer Science.” In Conceptual Structures: Integration and Interfaces, Lecture Notes in Computer Science Volume 2393, 2002, 2-19
In the last years, the main orientation of Formal Concept Analysis (FCA) has turned from mathematics towards computer science. This article provides a review of this new orientation and analyzes why and how FCA and computer science attracted each other. It discusses FCA as a knowledge representation formalism using five knowledge representation principles provided by Davis, Shrobe, and Szolovits [15]. It then studies how and why mathematics-based researchers got attracted by computer science. We will argue for continuing this trend by integrating the two research areas FCA and Ontology Engineering.

C. Sacarea, “Towards a Contextual Topology”, Proceedings of the Algebra Symposium “Babe ̧s-Bolyai” University Cluj, 2002, 239-251.

J.L. Ramı́rez Alfonsı́n, David Romero, “Embeddability of the combinohedron”, Discrete Mathematics, Volume 254, Issues 1–3, 10 June 2002, 473-483

R. Wille, “Sind unsere Vorstellungen von Raum und Zeit richtig? oder: Besteht ein Kontinuum aus Punkten?” In: Hefendehl-Hebeker, L., Hußmann, S., (Hrsg.): Mathematikdidaktik: Zwischen Fachorientierung und Empirie. Franzbecker Verlag, Hildesheim, 2003, 266-279.

R. Wille, “Conceptual Contents as Information – Basics for Contextual Judgment Logic”, in 11th International Conference on Conceptual Structures, ICCS 2003, Dresden, Germany, July 21-25, 2003.
In Contextual Judgment Logic, Sowa’s conceptual graphs (understood as graphically structured judgments) are made mathematically explicit as concept graphs which represent information formally based on a power context family and rhetorically structured by relational graphs. The conceptual content of a concept graph is viewed as the information directly represented by the graph together with the information deducible from the direct information by object and concept implications coded in the power context family. The main result of this paper is that the conceptual contents can be derived as extents of the so-called conceptual information context of the corresponding power context family. In short, the conceptual contents of judgments are formally derivable as concept extents.

R. Wille, “Dyadic Mathematics – Abstractions from Logical Thought.” In: K. Denecke, M. Erné, S.L. Wismath (eds.): Galois Connections and Applications, Kluwer, 2004
An important question is how mathematics may support human thinking about the real world. Since human thinking is based on concepts grasping realities, an appropriate mathematization of concepts and conceptual relationships may give a useful foundation for connecting mathematical thoughts with the reality-oriented thinking of human beings. The mathematization of concepts based on formal contexts has been matured over twenty years and proven to be useful in many aspects; in particular, the Galois connection between the extensional and the intensional view gave a strong backbone for connecting mathematics with real world issues. This even suggested to unify the two views in mathematical theory building to obtain what might be called "Dyadic Mathematics". This idea shall be illustrated by some examples of using Galois connections.

Th. Noll and M. Brand, “Morphology of Chords,” In G. Mazzola, Th. Noll, E. Lluis-Puebla, Perspectives in Mathematical and Computational Music Theory, epOs-Music, Osnabrück 2004, 366-398.

D. Lewin, “Some compositional uses of projective geometry,” Perspectives of New Music, 42, 2004, 12–63.

R. Wille, “Formal Concept Analysis as Mathematical Theory of Concepts and Concept Hierarchies”. In Ganter et al. (eds), Formal Concept Analysis, LNAI 3626, 2005, 1-33.
Formal Concept Analysis has been originally developed as a subfield of Applied Mathematics based on the mathematization of concept and concept hierarchy. Only after more than a decade of development, the connections to the philosophical logic of human thought became clearer and even later the connections to Piaget’s cognitive structuralism which Thomas Bernhard Seiler convincingly elaborated to a comprehensive theory of concepts in his recent book [Se01]. It is the main concern of this paper to show the surprisingly rich correspondences between Seiler’s multifarious aspects of concepts in the human mind and the structural properties and relationships of formal concepts in Formal Concept Analysis. These correspondences make understandable, what has been experienced in a great multitude of applications, that Formal Concept Analysis may function in the sense of transdisciplinary mathematics, i.e., it allows mathematical thought to aggregate with other ways of thinking and thereby to support human thought and action.

F. Dau and J. Klinger, “From Formal Concept Analysis to Contextual Logic.” In Ganter et al. eds, 2005.
A main goal of Formal Concept Analysis from its very beginning has been the support of rational communication. The source of this goal lies in the understanding of mathematics as a science which should encompass both its philosophical basis and its social consequences. This can be achieved by a process named ‘restructuring’. This approach shall be extended to logic, which is based on the doctrines of concepts, judgments, and conclusions. The program of restructuring logic is named Contextual Logic (CL). A main idea of CL is to combine Formal Concept Analysis and Concept Graphs (which are mathematical structures de- rived from conceptual graphs). Concept graphs mathematize judgments which combine concepts, and conclusions can be drawn by inferring concept graphs from others. So we see that concept graphs can be understood as a crucial part of the mathematical implementation of CL, based on Formal Concept Analysis as the mathematization of the doctrine of concepts.

R. Wille, “Contextual Logic and Aristotle’s Syllogistic.” In 13th International Conference on Conceptual Structures, ICCS 2005, Kassel, Germany, July 17-22, 2005.
This paper is concerned with incorporating negational relationships into the semantics of Contextual Logic by mathematizing Aristotle’s Syllogistic in contextual-logic terms. For preparing this, a short sketch of Aristotle’s Syllogistic is presented. Then it is shown how a contextual semantics for Aristotle’s syllogisms can be developed on the basis of so-called syllogistic contexts. This semantic approach is used to determine implication bases for elementary judgments within syllogistic contexts. Finally, directions of further research are mentioned.

M. Krötzsch, Morphisms in Logic, Topology, and Formal Concept Analysis, thesis, TU Dresden 2005.
The general topic of this thesis is the investigation of various notions of morphisms between logical deductive systems, motivated by the intuition that additional (categorical) structure is needed to model the interrelations of formal specifications. This general task necessarily involves considerations in various mathematical disciplines, some of which might be interesting in their own right and which can be read independently. To find suitable morphisms, we review the relationships of formal logic, algebra, topology, domain theory, and formal concept analysis (FCA). This leads to a rather complete exposition of the representation theory of algebraic lattices, including some novel interpretations in terms of FCA and an explicit proof of the cartestian closedness of the emerging category. It also introduces the main concepts of «domain theory in logical form» for a particularly simple example. In order to incorporate morphisms from FCA, we embark on the study of various context morphisms and their relationships. The discovered connections are summarized in a hierarchy of context morphisms, which includes dual bonds, scale measures, and infomorphisms. Finally, we employ the well-known means of Stone duality to unify the topological and the FCA-based approach. A notion of logical consequence relation with a suggestive proof theoretical reading is introduced as a morphism between deductive systems, and special instances of these relations are identified with morphisms from topology, FCA, and lattice theory. Especially, scale measures are recognized as topologically continuous mappings, and infomorphisms are identified both with coherent maps and with Lindenbaum algebra homomorphisms.

M. Krötzsch, P. Hitzler, G.-Q. Zhang, “Morphisms in Context.” In Frithjof Dau, Marie-Laure Mugnier, Gerd Stumme, eds.: Proceedings of the 13th International Conference on Conceptual Structures (ICCS-05), Springer 2005.
Morphisms constitute a general tool for modelling complex relationships between mathematical objects on a large scale. In Formal Concept Analysis (FCA), morphisms can therefore be used for the study of structural properties of the knowledge represented in formal contexts, with applications to data transformation and merging. In this paper we present a comprehensive treatment of some of the most important morphisms in FCA and their relationships, which includes the study of dual bonds, scale measures, infomorphisms and their respective relations to Galois connections. We summarize our results in a concept lattice that displays all relationships between the considered morphisms. The purpose of this foundational work is to provide a basis for future applications of FCA in ontology research and similar areas, where morphisms provide a way to formalize the interplay between distributed knowledge bases.

R. Wille, “Methods of Conceptual Knowledge Processing,” 2006
The offered methods of Conceptual Knowledge Processing are procedures which are well-planed to mean and purpose and therewith lead to skills for solving practical tasks. The used means and skills have been mainly created as translations of mathematical means and skills of Formal Concept Analysis. Those transdisciplinary translations may be understood as transformations from mathematical thinking, dealing with potential realities, to logical thinking, dealing with actual realities. Each of the 38 presented methods is discussed in a general language of logical nature, while citations give links to the underlying mathematical background. Applications of the methods are demonstrated by concrete examples mostly taken from the literature to which explicit references are given.

P. Hitzler, M. Krötzsch, G.-Q. Zhang, “A Categorical View on Algebraic Lattices in Formal Concept Analysis.” In Fundamenta Informaticae 74 (2–3), IOS Press, 2006.
Formal concept analysis has grown from a new branch of the mathematical field of lattice theory to a widely recognized tool in Computer Science and elsewhere. In order to fully benefit from this theory, we believe that it can be enriched with notions such as approximation by computation or representability. The latter are commonly studied in denotational semantics and domain theory and captured most prominently by the notion of algebraicity, e.g. of lattices. In this paper, we explore the notion of algebraicity in formal concept analysis from a category-theoretical perspective. To this end, we build on the the notion of approximable concept with a suitable category and show that the latter is equivalent to the category of algebraic lattices. At the same time, the paper provides a relatively comprehensive account of the representation theory of algebraic lattices in the framework of Stone duality, relating well-known structures such as Scott information systems with further formalisms from logic, topology, domains and lattice theory.

M. J. Healy, Th. P. Caudell, “Ontologies and Worlds in Category Theory: Implications for Neural Systems,” Axiomathes 2006 03/06, 16(1-2), 165-214
We propose category theory, the mathematical theory of structure, as a vehicle for defining ontologies in an unambiguous language with analytical and constructive features. Specifically, we apply categorical logic and model theory, based upon viewing an ontology as a sub-category of a category of theories expressed in a formal logic. In addition to providing mathematical rigor, this approach has several advantages. It allows the incremental analysis of ontologies by basing them in an interconnected hierarchy of theories, with an operation on the hierarchy that expresses the formation of complex theories from simple theories that express first principles. Another operation forms abstractions expressing the shared concepts in an array of theories. The use of categorical model theory makes possible the incremental analysis of possible worlds, or instances, for the theories, and the mapping of instances of a theory to instances of its more abstract parts. We describe the theoretical approach by applying it to the semantics of neural networks.

P. Gehring, R. Wille, “Semantology: Basic Methods for Knowledge Representations.” In 14th International Conference on Conceptual Structures, ICCS 2006, Aalborg, Denmark, July 16-21, 2006. Proceedings
In this paper, we introduce the term “Semantology” for naming the theory of semantic structures and their connections. Semantic structures are fundamental for representing knowledge which we demonstrate by discussing basic methods of knowledge representation. In this context we discuss why, in the field of knowledge representation, the term “Semantology” should be given preference to the term “Ontology”.

R. Wille, R. Wille-Henning, “Beurteilung von Musikstücken durch Adjektive: Eine begriffsanalytische Exploration.” In: Proost, K. (ed.) Von Intentionalität zur Bedeutung Konventionalisierter Zeichen: Festschrift für Gisela Harras zum 65. Geburtstag, Studien Zur Dtsch. Sprache. G. Narr, Tübingen, 35, 2006, 453

B. Ganter, “Relational Galois Connections.” In Sergei O. Kuznetsov, Stefan Schmidt (eds), 5th International Conference, ICFCA 2007, Clermont-Ferrand, France
Galois connections can be defined for lattices and for ordered sets. We discuss a rather wide generalisation, which was introduced by Weiqun Xia and has been reinvented under different names: Relational Galois connections between relations. It turns out that the generalised notion is of importance for the original one and can be utilised, e.g., for computing Galois connections. The present paper may be understood as an attempt to bring together ideas of Wille [15], Xia [16], Domenach and Leclerc [3], and others and to suggest a unifying language.

P. Eklund, R. Wille, “Semantology as Basis for Conceptual Knowledge Processing” In Sergei O. Kuznetsov, Stefan Schmidt (eds), ICFCA 2007, Clermont-Ferrand, France, 2007.
Semantology has been introduced as the theory of semantic structures and their connections which, in particular, covers the methodology of activating semantic structures for representing conceptual knowledge. It is the main aim of this paper to explain and demonstrate that semantic structures are in fact basic for conceptual knowledge processing which comprises activities such as representing, infering, acquiring, and communicating conceptual knowledge.

J. J. Hennessy, “Partition Lattices in Milton Babbitt's Woodwind Quartet.” Journal of Mathematics and Music 1(3) (2007), 139-155.

E. Thul, Some Compositional Uses of Lattice Theory, Report, April 23, 2007 (pdf)

R. Wille and Renate Wille-Henning, “Towards a Semantology of Music.” In U. Priss, S. Polovina, and R. Hill (Eds.), Proceedings of the International Conference on Conceptual Structures, LNAI, Springer, 2007, 269-282.
The aim of this paper is to approach a Semantology of Music which is understood as the theory and methodology of musical semantic structures. The analysis of music structures is based on a threefold semantics which is performed on the musical level, the abstract philosophic-logical level, and the hypothetical mathematical level. Basic music structures are discussed by examples, in particular: tone systems, chords, harmonies, scales, modulations, musical time flow, and music forms. A specific concern of this paper is to clarify how a Semantology of Music may support the understanding of music.

R. Wille, “Transdisciplinarity and Generalistic Sciences and Humanities,” ICCS 2008
The term “transdisciplinarity” applies to forms of research which are used by disciplines with the effect that their ways of thinking are rationally understandable, available, and can be activated beyond their boundaries for being able especially to contribute to solutions of problems which cannot be mastered purely disciplinary. This paper elaborates the thesis that the disciplines can fulfill best the request for transdisciplinarity if they develop, maintain, and activate their part of generalistic sciences and humanities in the largest possible breath. For the transdisciplinary border crossing in the sense of generalistic sciences and humanities, it has been proven efficient to search for general interpretations of disciplinary concepts, propositions, and theories which can be made understandable (possibly in standard language). Examples are given by applications of Formal Concept Analysis.

R. Wille, “Communicative Rationality, Logic, and Mathematics,” ICFCA 2008
In this article the following thesis is explained and substantiated: Sense and meaning of mathematics finally lie in the fact that mathematics is able to support the rational communication of humans. The essence of the argumentation is that the effective support becomes possible by the close connection between mathematics and logic (in the sense of Peirce’s late philosophy) by which, in his turn, the commu- nicative rationality (in the sense of Habermas’ theory of communicative action) can be activated. How such a support may be concretely per- formed shall be illustrated by the development of a retrieval system for the library of the Center of Interdisciplinary Technology Research at Darmstadt University of Technology.

R. Wille, “An Algebraization of Linear Continuum Structures.” In Raoul Medina, Sergei Obiedkov (eds), ICFCA 2008, Montreal, Canada, 2008.
This paper continuous the approach of developing an order- theoretic structure theory of one-dimensional continuum structures as elaborated in [Wi07] (see also [Wi83],[Wi03]). The aim is to extend the order-theoretic structure theory by a meaningful algebraization; for this, we concentrate on the real linear continuum structure with its derived concept lattice which gives rise to the so-called “real half-numbers”. The algebraization approaches an ordered algebraic structure on the set of all real half-numbers to make the continuum structure of the reals more transparent and tractable.

R. Wille, “The Mathematical in Music Thinking”, CLA, 2008
“The Mathematical in music thinking” is based on Heidegger’s understanding of “the Mathematical” as the basic assumption of the knowledge of the things. Heidegger’s ideas are combined with Peirce’s classification of sciences, in particular, to distinguish between the Mathematical from the less abstract logical thinking and the more abstract mathematical thinking. The aim of this paper is to make understandable the role of the Mathematical in music. The paper concentrates on three domains: the rhythmic of music, the doctrine of music forms, and the theory of tonal systems. The theoretical argumentations are assisted by musical examples: the Adagio of Mozart’s string quartet C major (KV 465), the second movement of Webern’s Symphony op.21, and a cadence illustrating the problem of the harmony of second degree.

R. Wille, “Human Being and Mathematics. Logical and Mathematical Thinking,” ICCS 2009
Logical thinking as an expression of human reason grasps the actual re- ality by the basic forms of thinking: concept, judgment, and conclusion. Mathematical thinking abstracts from logical thinking to disclose a cosmos of forms of potential realities hypothetically. Mathematics as a form of mathematical thinking can therefore support humans within their logical thinking about realities which, in particular, pro- motes sensible actions. This train of thought has been convincingly differentiated by Peirce’s philosophical pragmatism and concretized by a “contextual logic” invented by members of the mathematics department at the TU Darmstadt.

D. Borchmann, B. Ganter, “Concept Lattice Orbifolds – First Steps.” In Sébastien Ferré, Sebastian Rudolph (eds.), ICFCA 2009, Darmstadt, Germany, 2009
Concept lattices with symmetries may be simplified by “folding” them along the orbits of their automorphism group. The resulting diagram is often more intuitive than the full lattice diagram, but well defined annotations are required to make the folded diagram as informative as the original one. The folding procedure can be extended to formal contexts. A typical situation where such lattice foldings are useful is when hierarchies of structures are considered “up to isomorphisms”.

F. Dau, “The Advent of Formal Diagrammatic Reasoning Systems.” In Sébastien Ferré, Sebastian Rudolph (eds.), ICFCA 2009, Darmstadt, Germany, 2009
In knowledge representation and reasoning systems, diagrams have many practical applications and are used in numerous settings. Indeed, it is widely accepted that diagrams are a valuable aid to intuition and help to convey ideas and information in a clear way. On the other side, logicians have viewed diagrams as informal tools, but which cannot be used in the manner of formal argumentation. Instead, logicians focused on symbolic representations of logics. Recently, this perception was overturned in the mid 1990s, first with seminal work by Shin on an extended version of Venn diagrams. Since then, certainly a growth in the research field of formal reasoning with diagrams can be witnessed. This paper discusses the evolution of formal diagrammatic logics, focusing on those systems which are based on Euler and Venn-Peirce diagrams, and Peirces existential graphs. Also discussed are some challenges faced in the area, some of which are specifically related to diagrams.

M. Krötzsch and B. Ganter, “A Brief Introduction to Formal Concept Analysis.” In P. Hitzler, H. Scharfe (eds), Conceptual Structures in Practice, Chapman and Hall/Crc Studies in Informatics Series, 2009

J. F. Sowa, “Conceptual Graphs for Representing Conceptual Structures.” In P. Hitzler, H. Scharfe (eds), Conceptual Structures in Practice, Chapman and Hall/Crc Studies in Informatics Series, 2009

R. Wille, “Formal Concept Analysis and Contextual Logic.” In P. Hitzler, H. Scharfe (eds), Conceptual Structures in Practice, Chapman and Hall/Crc Studies in Informatics Series, 2009

J. Th. Winkler, Algebraische Modellierung von Tonsystemen. Musiktheorie mit mathematischen Mitteln, Beiträge zur Begrifflichen Wissensverarbeitung, Verlag Allgemaine Wissenschaft, Mühltal, 2009

T. Motoyoshi, H. Kawakami, T. Shiose, O. Katai, "Formal Concept Analysis of Musicians’ Awareness for Musical Expression" in Proceedings of the 7th Triennial Conference of European Society for the Cognitive Sciences of Music (ESCOM 2009) Jyväskylä, Finland Jukka Louhivuori, Tuomas Eerola, Suvi Saarikallio, Tommi Himberg, Päivi-Sisko Eerola (Editors) (pdf)

F. Dau, “Die Ikonizität der Peirceschen Existentiellen Graphen aus der Sicht der Formalen Logik.” In Roland Posner, Stephan Debus (eds): Zeitschrift für Semiotik, 31 Issue 3-4/2009, 2011, Stauffenburg Verlag, Tübingen.

R. Wille, “Mathematics. Presenting, Reflecting, Judging,” ICFCA 2010
To understand what it means to present, to reflect, and to discuss mathematics, mathematics shall in the first place be characterized in connection of Peirce’s classification of the inquiring sciences. The threefold view of the universal categories of Peirce suggests to orientate the expositions – for presenting on the self-image of mathematics (as a First), – for reflecting on the relationship of mathematics to the real world (as a Second), and – for judging on the sense, meaning and connection of mathematics (as a Third). These expositions support the following basic thesis: sense and meaning of mathematics finally lie in the fact, that mathematics may effectively support the rational communication of human beings.

M. J. Healy, “Category Theory as a Mathematics for Formalizing Ontologies,” Theory and Applications of Ontology: Computer Applications 2010, 487-510
Category theory is discussed as an appropriate mathematical basis for the formalization and study of ontologies. It is based upon the notion of the structure manifest in systems of compositional relations and through mappings between systems that preserve composition. With one or two important exceptions, the basic concepts of category theory needed for an understanding of the other chapters involving category theory are presented here. The exceptions will be presented where they are used.

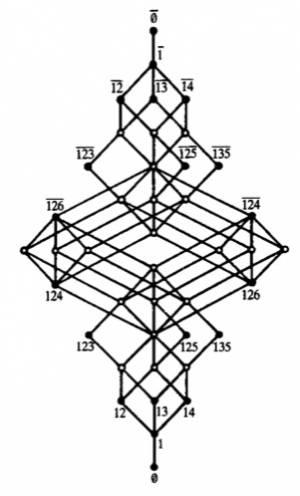
T. Schlemmer, S. E. Schmidt, “A Formal Concept Analysis of Harmonic Forms and Interval Structures,” Annals of Mathematics and Artificial Intelligence, June 2010, 59(2), 241-256
While small concept lattices are often represented by line diagrams to better understand their full structure, large diagrams may be too complex to do this. However, such a diagram may still be used to receive new ideas about the inherent structure of a concept lattice. This will be demonstrated for a certain family of formal contexts arising from mathematical musicology. In particular, we investigate how chord patterns can be characterised by their interval structure. For such contexts of pattern structures, it turns out that each corresponding concept lattice incorporates two competing building principles, one emanating from the top the other from the bottom of the lattice.

R. Wille, “Formal Concept Analysis of Two-Dimensional Convex Continuum Structures,” ICFCA 2010
This paper offers an approach of developing an order- theoretic structure theory of two-dimensional convex continuum structures. The chosen approach is based on convex planar continua and their subcontinua as primitive notions. In a first step convex planar continua are mathematized and represented by ordered sets. In a second step ‘points’ are deduced as limits of continua by methods of Formal Concept Analysis. The convex continuum structures extended by those points give rise to complete atomistic lattices the atoms of which are just the smallest points. Further research is planned to extend the approach of this paper to higher dimensional continuum structures.

Z. Marian and Ch. Sacarea, "Discovering Patterns in Music. An FCA Grounded Approach", Studia Univ. Babes-Bolyai, Informatica, vol LV, N. 1, 2010
We apply methods of Formal Concept Analysis in order to discover patterns in modern music. For this, we investigate the Music Genome, a project started on the 6th of January 2000 by a group of musicians and music-loving technologists who came together with the idea of creating the most comprehensive analysis of music ever. We also present an environment for processing and representation of music patterns.

J. O. Martins, “Pitch-Space Lattices: Tonnetze and other Transpositional Networks,” Bridges, 2011 (pdf)

J. Estrada, “La teorıa d1, MuSIIC-Win y algunas aplicaciones al analisis musical: Seis piezas para piano, de Arnold Schoenberg”, in Memoirs of the Fourth International Seminar on Mathematical Music Theory, Emilio Lluis-Puebla Octavio A. Agustín-Aquino (Editors), Memorias. Vol. 4 (2011) (pdf)

R. Wille, “Conceptual Knowledge Processing: Theory and Practice,” 2011
Conceptual Knowledge Processing is understood as the general scientific discipline which activitates acts of thinking such as representing, reasoning, acquiring, and communicating conceptual knowledge. In this contribution, first a short introduction to the foundation of Conceptual Knowledge Processing is presented. Then the theoretical background based on Formal Concept Analysis is sketched. The main content of this contribution is a discussion of the practice of Conceptual Knowledge Processing which demonstrates for twelve selected general acts of thinking how they can be successfully applied by using different methods of Conceptual Knowledge Processing.

R. Wille, “Mathematik semantologisch verstehen,” in Mathematik Verstehen, 2011, 87-102
Um zu verstehen, was Mathematik ist und bedeutet, reicht es nicht aus, mathematisches Denken und Wissen vielseitig zu erwerben. Hinzukommen muss stets ein angemessenes Verständnis der jeweiligen Bedeutungen mathematischer Denkformen, die in der aktual-realen Welt wirksam werden können. Beim Mathematik-Verstehen sollte es vor allem um ein Vermitteln des Selbstverständnisses der Mathematik, um ein Reflektieren des Bezugs der Mathematik zur realen Welt und um ein Beurteilen von Sinn, Bedeutung und Zusammenhang des Mathematischen in der Welt gehen.

M. Pendergrass, “Two Musical Orderings,” preprint, 2012 (html)
We make some general observations about partial orders on quotient spaces, and explore their use in music theory, in two different contexts. In the first, we show that many of the most familiar chord and scale types in Western music appear as extremal elements in the partial order induced by set inclu- sion on pitch class sets of Tn type. In the second, we propose a partial order that models the brightness aspect of timbre. We use this order to compare the brightness of six wind instruments, and find that the results conform to intuition. We also use the order to pose sound design problems of a certain type, which can be solved efficiently using linear programming.

T. Schlemmer, “Annotating Lattice Orbifolds with Minimal Acting Automorphisms,” 2012.
Context and lattice orbifolds have been discussed by M. Zickwolff [1,2], B. Ganter and D. Borchmann [3,4]. Preordering the folding automorphisms by set inclusion of their orbits gives rise to further development. The minimal elements of this preorder have a prime group order and any group element can be dissolved into the product of group elements whose group order is a prime power. This contribution describes a way to compress an orbifold annotation to sets of such minimal automorphisms. This way a hierarchical annotation is described together with an interpretation of the annotation. Based on this annotation an example is given that illustrates the construction of an automaton for certain pattern matching problems in music processing.

L. Amgoud, H. Prade, “Argumentation abstraite et concepts formels. A formal concept view of abstract argumentation”, preprint, 2012 (pdf)

D. Dubois, H. Prade, “From Blanché’s Hexagonal Organization of Concepts to Formal Concept Analysis and Possibility Theory”, Logica Universalis, June 2012, 6(1-2), 149-169
The paper first introduces a cube of opposition that associates the traditional square of opposition with the dual square obtained by Piaget’s reciprocation. It is then pointed out that Blanché’s extension of the square-of-opposition structure into an conceptual hexagonal structure always relies on an abstract tripartition. Considering quadripartitions leads to organize the 16 binary connectives into a regular tetrahedron. Lastly, the cube of opposition, once interpreted in modal terms, is shown to account for a recent generalization of formal concept analysis, where noticeable hexagons are also laid bare. This generalization of formal concept analysis is motivated by a parallel with bipolar possibility theory. The latter, albeit graded, is indeed based on four graded set functions that can be organized in a similar structure.

NEWS

• Th. Noll, Diatonische Modi als Automorphismen der freien Gruppe F_2 (Seminar, TU Dresden, 30 November 2012)
• Gesprächsveranstaltung "Wie denken wir Musik? - Kompositorische und mathematische Perspektiven", 29. November 2012 um 15:30, Studio für Elektronische Musik der Hochschule für Musik Carl Maria von Weber Dresden Raum W 3.19. Avec la participation d'Immanuel Albrecht (TU-Dresden), Moreno Andretta (IRCAM Paris), Christoph Mann (HfM-Dresden), Maximilian Marx (TU-Dresden), Thomas Noll (ESMuC, Barcelona), Franz Martin Olbrisch (HfM-Dresden), Tobias Schlemmer (TU-Dresden), Stefan Schmidt (TU-Dresden) - (info)
• M. Andreatta, On two open mathematical problems in music theory: Fuglede spectral conjecture and discrete phase retrieval (Seminar, TU Dresden, 29 Novembre 2012) - Abstract + biblio
• Festkolloquium en honneur de Rudolf Wille (à l'occasion de son 75e anniversaire), Ernst-Schröder-Zentrum für begriffliche Wissensverarbeitung, Darmstadt, 9 November 2012) - (pdf)