On two open mathematical problems in music theory: Fuglede spectral conjecture and discrete phase retrieval

(Seminar, TU Dresden, 29 Novembre 2012)

Abstract

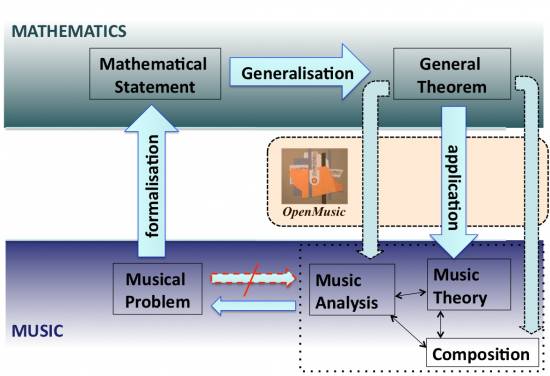
After briefly presenting the underlying philosophy of “mathemusical” research which we carry on at IRCAM/Paris (from music to mathematics to computer-aided music theory, analysis and composition), and providing a short list of theoretical problems on which we have been working in the last years (see [1] for a detailed presentation), we focus on two open mathematical problems: Fuglede (or Spectral) Conjecture and the Discrete Phase Retrieval problem.

The first conjecture, originally appeared in [2], states the equivalence between spectral property of a domain of the n-dimensional Euclidean space and its tiling character. The conjecture, which is false for n≥3, is still open for n=1 and n=2. We will discuss the case n=1 by showing its deep relationships with a musical compositional process – the rhythmic tiling canons construction – via a much older geometric and number-theoretical conjecture, i.e. Minkowski’s Conjecture. This conjecture, raised by Minkowski in [3] and solved by Hajós almost forty years later [4], states that every lattice tiling of the n-dimensional Euclidean space by unit hypercubes contains two cubes that meet in an (n-1)-dimensional face. (See [5] and [6] for some recent perspectives on this first mathematical conjecture and its music-theoretical ramifications).

The second mathematical problem deals with the possibility of reconstruct a set by knowing its inter-point distances. It shows the deep connections between the notion of Z-relation in music theory – i.e. the property of two subsets of a cyclic group of having the same interval content, as originally introduced by Hanson in [7] and successively formalized by Forte [8] and Lewin [9] – and the theory of homometric sets in crystallography [10]. We will describe some aspects of phase-retrieval approaches in music by focusing on the particular case of the cyclic groups (beltway problem) and discussing the extended phase retrieval for a generalized musical Z-relation [11]. Some musical examples will finally show the relationships between these two open mathematical problems via OpenMusic, a Visual Progamming Language for computer-aided music theory analysis and composition currently developed by IRCAM Music Representation Team [12].

References:

1. M. Andreatta, Mathematica est exercitium musicae: la recherche "mathémusicale" et ses interactions avec les autres disciplines, Habilitation thesis, IRMA (Institut de Recherche Mathématique Avancée, University of Strasbourg), 2010 (pdf)
2. B. Fuglede, "Commuting Self-Adjoint Partial Differential Operators and a Group Theoretic Problem." J. Func. Anal. 16, 101-121, 1974
3. H. Minkowski, Minkowski, Diophantische Approximationen. Leipzig, Teubner, 1907.
4. G. Hajós, G. "Über einfache und mehrfache Bedeckung des n-dimensionalen Raumes mit einen Würfelgitter." Math. Z. 47, 427-467, 1942.
5. M. Andreatta, C. Agon (eds), Tiling Problems in Music, Special Issue of the Journal of Mathematics and Music, July 2009, 3(2), 63-70 (Guest Editor’s Foreword)
6. M. Andreatta, “Constructing and Formalizing Tiling Rhythmic Canons : A Historical Survey of a ‘Mathemusical’ Problem,” Perspectives of New Music, Special Issue, 49(1-2), 2011 (pdf)
7. H. Hanson, Harmonic Materials of Modern Music, Appleton-Century-Crofts, New York, 1960.
8. A. Forte, The Structure of Atonal Music, Yale University Press, New Haven, 1973.
9. D. Lewin, Generalized Musical Intervals and Transformations, Yale University Press, New Haven, 1987 (2nd ed., Oxford University Press, Oxford, 2007).
10. J. Mandereau, D. Ghisi, E. Amiot, M. Andreatta, C. Agon, “Z-relation and homometry in musical distributions,” Journal of Mathematics and Music, 5(2), 83-98, 2011 (pdf)
11. J. Mandereau, D. Ghisi, E. Amiot, M. Andreatta, C. Agon, “Discrete Phase Retrieval in Musical Structures,” Journal of Mathematics and Music, 5(2), 99-116 (pdf)
12. OpenMusic : http://repmus.ircam.fr/openmusic/home

pdf version

Contact

Moreno ANDREATTA
CNRS Researcher
Music Representation Team
Ircam - CNRS UMR 9912 (STMS)
1, place I. Stravinsky
F-75004 Paris
tel:+33 (0)1 44781649
e-mail : Moreno.Andreatta[at]ircam.fr

(back to the Formal Concept Analysis applied to Music webpage)