Piste: • smir

SMIR - Structural Music Information Research (resp. Moreno Andreatta)

smir_scheme_mathsmusic.jpg CNRS Director of Research at IRMA and member of the CREAA
University of Strasbourg
7 rue René-Descartes / F-67084 Strasbourg
e-mail : andreatta[at]math.unistra.fr

Former acting President of the SMCM and head of the SMIR Project
Associate researcher at the Music Representation Team
IRCAM - CNRS UMR 9912 (STMS) - Sorbonne Université
1, place I. Stravinsky / F-75004 Paris
tel:+33 (0)1 44781488
e-mail : Moreno.Andreatta[at]ircam.fr

Le greffon Adobe Flash est nécessaire pour afficher ce contenu.


Short description:

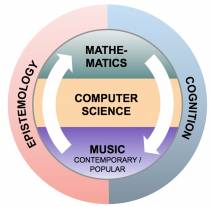
Despite a long historical relationship between mathematics and music, the interest of mathematicians is a recent phenomenon. In contrast to statistical methods and signal-based approaches currently employed in Music Information Research, the SMIR project stresses the necessity of introducing a structural multidisciplinary approach into computational musicology making use of advanced mathematics. The project is based on the interplay between three main mathematical disciplines: algebra, topology and category theory. It therefore opens promising perspectives on important prevailing challenges, such as the automatic classification of musical styles or the solution of open mathematical conjectures, asking for new collaborations between mathematicians, computer scientists, musicologists, and composers.

The SMIR project also differs from traditional applications of mathematics to music in aiming to build bridges between different musical genres, ranging from contemporary art music to popular music, including rock, pop, jazz and chanson. It aims to create a unique research environment at the University of Strasbourg where mathematicians will collaborate with computer scientists, musicologists and composers. New structural mathematical methods based on algebra, topology and category theory are proposed in order to reveal musical properties, thus opening strategic research directions in computational musicology via a genuinely multidisciplinary approach. They will be integrated into a unique pedagogical software tool strongly reinforcing the scientific and pedagogical outreach. If mathematics has largely shown its power and generality in music theory and analysis, the SMIR project claims that the opposite also holds. Music can occupy a strategic place in the development of mathematics since music-theoretical constructions can be used to solve open mathematical problems.

The SMIR project will also contribute to the emergence of a new structural approach in the field of Music Information Research based on the interplay between different mathematical disciplines such as algebra, topology and category theory. It proposes to approach the computational aspects of musical processes in a unifying way by removing the boundaries between different genres and by paying equal attention to contemporary art music and popular music. The development of ad-hoc computer-aided environments is a necessary condition to enable the systematic comparison between theoretical constructions and computational models. This will not only open new forms of collaborations between mathematicians, computer scientists, musicologists and composers, but will also provide an important contribution to the emergence of new pedagogical approaches in “mathemusical” research which will help to spread this interdisciplinary research outside of the circle of specialists.


Main research axes:

  • Mathematical Morphology, Formal Concept Analysis and computational musicology (see [12], [8],[18], [20], [31], [41], [42])
  • Generalized Tonnetze, Persistent Homology and automatic classification of musical styles (see [16], [17], [11], [13], [9], [26], [28], [29], [30], [32], [33], [35], [36], [37], [38])
  • Category theory and transformational (computer-aided) music analysis (see [15], [19], [23], [2], [24], [25], [27], [40])
  • Music-theoretical problems and open conjectures in mathematics ([10], [3], [4], [1], [34])
  • Epistemological and cognitive aspects of mathemusical research ([16], [6], [5], [7], [14], [22], [38])


Some references:

  • [1] Lachaussée, G. (2010) Théorie des ensembles homométriques, Stage de troisième année de l'Ecole Polytechnique, Master 1 de Mathématiques. (pdf)
  • [2] Fiore T., Noll Th. (2011), "Commuting Groups and the Topos of Triads", in C. Agon et al. (eds), Proceedings of the Third international conference on Mathematics and computation in music (Paris, 15-17 June 2011), Springer LNCS/LNAI, p. 69-83 (draft version)
  • [3] Mandereau J., Ghisi D., Amiot E., Andreatta M., Agon C., (2011a), "Z-relation and homometry in musical distributions", Journal of Mathematics and Music, vol. 5, n° 2, p. 83-98. (pdf).
  • [4] Mandereau J., Ghisi D., Amiot E., Andreatta M., Agon C. (2011b), "Discrete phase retrieval in musical structures", Journal of Mathematics and Music, vol. 5, n° 2, p. 99-116 (pdf).
  • [5] Acotto E., Andreatta M. (2012), "Between Mind and Mathematics. Different Kinds of Computational Representations of Music", Mathematics and Social Sciences (50e année, n° 199, 2012(3), p. 9-26. Special Issue devoted to the Conference of the EMPG 2011 (European Mathematical Psychology Group, Telecom ParisTech, 29-31 août 2011). draft
  • [6] Andreatta M. (2012), "Mathématiques, Musique et Philosophie dans la tradition américaine : la filiation Babbitt/Lewin", in Andreatta M., F. Nicolas, Ch. Alunni dir. (2012), A la lumière des mathématiques et à l'ombre de la philosophie. Dix ans de séminaire mamuphi, Collection "Musique/Sciences", Ircam-Delatour France, Sampzon, p. 51-74. Draft.
  • [7] Andreatta, M., Ehresmann A., Guitart R., Mazzola G., (2013), "Towards a categorical theory of creativity", Proceedings of the Conference MCM 2013, McGill University, Montreal, June 12-14, 2013. Lecture Notes in Computer Science / LNAI, Springer, p. 19-37 (pdf)
  • [8] Schlemmer T., Andreatta M. (2013), "Using Formal Concept Analysis to Represent Chroma Systems", Proceedings of the Conference MCM 2013, McGill University, Montreal, June 12-14, 2013. Lecture Notes in Computer Science / LNAI, Springer, p. 189-200 (pdf).
  • [9] Bigo L., Ghisi D., Spicher A., Andreatta M. (2014), "Spatial Transformations in Simplicial Chord Spaces", in A. Georgaki and G. Kouroupetroglou (Eds.), Proceedings ICMC|SMC|2014, 14-20 September 2014, Athens, Greece, p. 1112-1119. Best paper award. (pdf).
  • [10] Andreatta, M. (2015), "Tiling Canons as a key to approach open Mathematical Conjectures ?", in E. Chew et al. (eds.), Mathemusical Conversations, Wiley, p. 86-104.
  • [11] Bergomi, M., (2015), Dynamical and topological tools for (modern) music analysis (PhD in cotutelle UPMC/LIM Milan, co-supervised with Goffredo Haus, December 2015 (pdf)
  • [12] Freund A., Andreatta M., Giavitto J.-L. (2015), "Lattice-based and Topological Representations of Binary Relations with an Application to Music", Annals of Mathematics and Artificial Intelligence, vol. 73, n° 3-4, p. 311-334. (pdf).
  • [13] Bigo L., Andreatta M. (2015), "Topological Structures in Computer-Aided Music Analysis", in D. Meredith (ed.), Computational Music Analysis, Springer, p. 57-80 - (pdf).
  • [14] Andreatta M. (2015), "Autour de la Set Theory et de l’analyse de la musique atonale : démarche structurale et approche phénoménologique à partir des écrits de Célestin Deliège", in Modernité musicale au XXe siècle et musicologie critique. Hommage à Célestin Deliège (Valérie Dufour and Robert Wangermée eds.), collection de l’Académie, Bruxelles, p. 93-110. (Draft).
  • [15] Popoff A., Andreatta M., Ehresmann A. (2015), "A Categorical Generalization of Klumpenhouwer Networks", Proceedings of the Conference MCM 2015, Queen Mary University, London, June 22-25, 2015. Lecture Notes in Computer Science / LNAI, Springer, p. 303-314 pdf
  • [16] Andreatta M., Baroin G. (2016), "Formal and Computational Models in Popular Music", Z. Kapoula (eds.), AEsthetics & Neurosciences: Scientific and Artistic Perspectives, Springer, p. 257-269 (pdf)
  • [17] Bergomi M., Fabbri F., Andreatta M. (2016), "Hey Maths ! Modèles formels et computationnels au service des Beatles", Volume ! La revue des musiques populaires (Grégoire Tosser and Olivier Julien editors), vol. 12, n° 2, p. 161-179 (Slides of the invited presentation by Moreno Andreatta at the Beatles Day, Evry, 6 November 2014)
  • [18] Relaño P. (2017), Morphologie mathématique, FCA et musicologie computationnelle, Master 2 maths-info, ENS-Lyon / LTCI/Télécom ParisTech / LAMSADE, Université Paris Dauphine / IRCAM-CNRS-UPMC), March-July 2017 - Dissertation and master thesis presentation
  • [19] Popoff A., Agon C., Andreatta M., Ehresmann A. (2017), "From K-Nets to PK-Nets: A Categorical Approach", Perspectives of New Music, 54(2), p. 5-63 draft version).
  • [20] Agon C., Andreatta M., Atif J., Bloch I., Mascarade P. (2018), "Musical Descriptions Based on Formal Concept Analysis and Mathematical Morphology", in P. Chapman et al. (eds), Graph-Based Representation and Reasoning, Proceedings of the 23rd International Conference on Conceptual Structures, ICCS 2018, p. 105-119 pdf.
  • [21] Andreatta, M. (2018), "From music to mathematics and backwards: introducing algebra, topology and category theory into computational musicology". In Michele Emmer and Marco Abate (eds.), Imagine Math 6 - Mathematics and Culture, XXth Anniversary, Springer, 2018, pp. 77-88.
  • [22] Besada L. (2018), "Sharing and Enacting Cognitive Metaphors in Musical Distributed Contexts: A Case Study from IRCAM", to appear in the Proceedings of the 15th International Conference on Music Perception and Cognition (ICMPC) and 10th Triennial Conference of the European Society for the Cognitive Sciences of Music (ESCOM), Montreal, Sydney, La Plata, and Graz, July 23–28 2018
  • [23] A. Popoff, "Towards A Categorical Approach of Transformational Music Theory", (unpublished manuscript)
  • [24] Fiore T., T. Noll, "Voicing Transformations and a Linear Representation of Uniform Triadic Transformations" (submitted. Arxiv version)
  • [25] Popoff A., M. Andreatta, A. Ehresmann (2018), "Relational PK-Nets for Transformational Music Analysis", Journal of Mathematics and Music, vol. 12, n° 1, p. 35-55 pdf.
  • [26] Lascabettes P. (2018), Homologie Persistante Appliquée à la Reconnaissance de Genres Musicaux, Master 1 mathématiques, ENS Paris Saclay / Université de Strasbourg (Cosupervised by C. Guichaoua and M. Andreatta) - pdf
  • [27] Popoff A., M. Andreatta, A. Ehresmann (2019), "Groupoids and Wreath Products of Musical Transformations: A Categorical Approach from poly-Klumpenhouwer Networks", in M. Montiel et al. (eds), Proceedings MCM 2019, Springer, pp. 33-45 pdf.
  • [28] Bigo L., M. Andreatta (2019), "Filtration of Pitch-Class Sets Complexes", in M. Montiel et al. (eds), Proceedings MCM 2019, Springer, pp. 213-226 pdf.
  • [29] Callet V. (2020), "Suites spctrales et homologie persistante", Master 2 Dissertation, Université de Strasbourg (under the supervision of Pierre Guillot) - pdf
  • [30] Bergomi M. (2020), "Homological persistence in time series: an application to music classification", Journal of Mathematics and Music, Vol. 14, Nr. 2, pp. 204-221) (Special Issue on Geometry and Topology in Music; Guest Editors: Moreno Andreatta, Emmanuel Amiot, and Jason Yust).
  • [31] Lascabettes, P., I. Bloch, C. Agon (2020), "Analyse de représentations spatiales de la musique par des opérateurs simples de morphologie mathématique", Journées d'Informatique Musicale, Strasbourg, 26-28 October 2020 - pdf
  • [32] Karystinaios E., C. Guichaoua, M. Andreatta, L. Bigo, I. Bloch (2020), "Music Genre Descriptor for Classification based on Tonnetz Trajectories", Journées d'Informatique Musicale, Strasbourg, 26-28 October 2020 - draft
  • [33] Guillaume Rousseau (2021), "Persistent Homology and Topological Data Analysis Applied to Music", Master 2 Dissertation, ENS-Lyon and University of Strasbourg (under the supervision of Moreno Andreatta) - pdf
  • [34] Luisa Fiorot, Alberto Tonolo, and Riccardo Gilblas (2022), "The Mystery of Anatol Vieru's Periodic Sequences Unveiled", Proceedings MCM 2022, p. 376-382 pdf.
  • [35] Maximilien Wang (2023), "Homologie persistante appliquée à la classification automatique des styles musicaux", Master 2 Dissertation, University of Bordeaux and University of Strasbourg (under the supervision of Moreno Andreatta) - pdf
  • [36] Paul Lascabettes, Mathematical Models for the Discovery of Musical Patterns, Structures and for Performances Analysis, IRCAM/University of Sorbonne (under the supervision of Isabelle Bloch and Elaine Chew) - pdf
  • [37] Victoria Callet, Topological modeling of musical structures and processes, PhD, University of Strasbourg (under the supervision of Pierre Guillot and Moreno Andreatta) - pdf
  • [38] Riccardo Gilblas, Periodic Sequences and Persistent Homology applied to Music. Theoretical Foundations and New Results, University of Padova and University of Strasbourg (under the supervision of Luisa Fiorot and Moreno Andreatta)
  • [39] José Luis Besada, Erica Bisesi, Corentin Guichaoua, Moreno Andreatta, "The Tonnetz at First Sight: Cognitive Issues of Human-Computer Interaction with Pitch Spaces", Music & Science, 7 - pdf
  • [40] Alexandre Popoff and Moreno Andreatta, "Hidden Categories: a new perspective on Lewin's Generalized Interval Systems and Klumpenhouwer Networks" (draft)
  • [41] Paul Lascabettes, Isabelle Bloch, « What Are "Good" Rhythms? Generating Rhythms Based on the Properties Set Out in The Geometry of Musical Rhythm », Proceedings Mathematics and Computation in Music, Springer, p. 45-57, 2024 (pdf).
  • [42] Paul Lascabettes, Isabelle Bloch, « Discovering Repeated Patterns From the Onsets in a Multidimensional Representation of Music », Discrete Geometry and Mathematical Morphology, 2024 (pdf).

Scientific production (Moreno Andreatta):

  • Publication track (with online versions of articles and conferences, including the list of supervised Master dissertations and PhD thesis)
  • Short curriculum vitae (2 pages, 2024) - pdf
  • Detailed curriculum vitae (2019-2023) - pdf

Future events:

  • Arts&Science Conference at the Journée Georges Bram 2025 (ENS Paris, January 10, 2025) - Programme
  • Math'n Pop @ Guebwiller (CCR Les Dominicains de Haute-Alsace, March 21, 2025) - info
  • Will you be interested to host the Math'n Pop show and related workshops? Please, do not hesitate to contact me!

Some recent presentations/performances:

  • "Some thoughts on new forms of contamination between contemporary and popular music: the role of mathematical formalization and computer-aided modeling" (conversation between Fabio Cifariello Ciardi and Moreno Andreatta at DiMMI 2024 (Dictionary for Multidisciplinary Music Integration), Trento (Italy), November 29-30 - Programme - slides.
  • Math'n Pop in Gorizia (Italy). The first representation of the Math'n Pop show in Italian! Auditorium of Gorizia, 28 November 2024, within an interdisciplinary Festival entitled "Intrecci musicali di frontiera" - Programme.
  • Math'n Pop at the Theater of the Reine Blanche (Paris, 12 November 2024). More info. New partnership with the CAES/CNRS.
  • IA and Music. A large public conference within the "Médiathèques en débat" event (Strasbourg, 6-16 November) - Programme - Talk (in pdf).
  • A series of talks at the Cagliari Festival of Science, Italy. A seminar within the cycle "Pomeriggi UniCAmente Matematici" (org. Prof. Paola Piu), a seminar on the history of mathematics and music (org. Prof. Maria Polo) and a large public presentation (moderated by Prof. Sonia Cannas).
  • Maths&Music at the Fête de la Science (Palais Universitaire, University of Strasbourg, 4-5 October 2024) - Some pictures pdf.
  • A Maths/Music Concert in Singapore (Yong Siew Toh Conservatory of Music, 19 Feb - 23 Feb 2024) - video - visual support. Complete program of MES 2024 (Mathemusical Encounters in Singapore: A Diderot Legacy)
  • Maths & Music at Guebwiller (12 March 2024). A short "avant-propos mathémusical" to Manu Houdart's Very Math Trip show at the CCR Les Dominicains de Haute-Alsace.
  • Math'n Pop at Wittenheim (16 February 2024). Organized by the SudAlsace Labo Maths (contact: Ezéchiel Rencker)
  • Moreno Andreatta, "Presentation of the Theory and Models research program at CREAA" - video
  • Moreno Andreatta, "Analysis and music informatics", masterclass at the Licence on Popular Music, Jazz and Chanson of the University of Bordeaux, November 17, 2023 (org. Pascal Pistone - slides - concert (at the Impromptu).
  • Moreno Andreatta, "A focus on some theoretical problems in contemporary 'mathemusical' research", Colloquium at the IMB, Bordeaux, November 16, 2023 (org. Andrea Fanelli) - slides
  • Moreno Andreatta, "Les maths dans la musique… la musique des maths !", large public conference, Centre de culture numérique, University of Strasbourg, November 15, 2023 - slides.
  • Moreno Andreatta, "Les maths dans la musique…la musique des maths !", concert-conference, IG–IA-IPR, Lycée Fustel de Coulanges, Strasbourg, September 28 - slides
  • José Luis Besada, Moreno Andreatta, "Neo-Riemannian tools for compositional adventures and empirical research", Music Theory & Artistic Research. 23rd Annual Conference of the Gesellschaft für Musiktheorie (GMTH), Freiburg University of Music (September 22-24, 2023) - Program - slides
  • Moreno Andreatta and Gilles Baroin, "Virtual Reality and 'mathemusical' research", Maths&Music Seminar, IRMA, Strasbourg, 23 June 2023.
  • "Maths in song writing: a focus on some Oumupian experiences", a concert-conference by Moreno Andreatta within the W&K-Forum: Symposium Musik & Mathematik (Salzburg, 2 June 2023. Organizers: Arne Bathke and Katarzyna Grebosz-Haring) - Programme - slides
  • Maths/Music at the Math.en.JEANS event (Mulhouse, 25 May 2023. Organizer: Nicolas Juillet) - Programme
  • Maths/Music at the Nuit des jeux mathématiques (Strasbourg, Le Vaisseau, 9 May 2023) - Interactive program
  • Cognitive Inspections of the Tonnetz: a multimodal approach. Conference by José Luis Besada (researcher at the Universidad Complutense of Madrid and invites researcher at IRMA) - Strasbourg, 9 May, 10am, MISHA (salle 140 Océanie)
  • Poetry, music and…maths! A concert-conference by Moreno Andreatta within the "Printemps des poètes" (Strasbourg, 25 March 2023). Under the auspices of the "Académie Rhénane" - Flyer
  • A Maths&Music Day at the Lycée Robert Schuman (10 March 2023, 9am-9pm), including a Concert-conference (with the students!) - Poster
  • A Maths&Music Webinar by Moreno Andreatta for Instant Science (9 March 2023, 8pm) - Registration - pdf
  • Andy Milne (USIAS invited researcher within the SMIR Project) will give a talk at the new IRMA-CREAA mathemusical seminar (Department of Mathematics, Strasbourg, 27 January 2022, 2pm)
  • "Tiling Rhythmic Canons. When Music meets Maths", invited talk at the Colloquium Series of the European Academy of Sciences and Arts (online, 13 January, 2023, 6pm)
  • "Transformational Music Theory: from group theory to film music analysis, and beyond…", talk by Alexandre Popoff at the IRMA-CREAA mathemusical seminar (Department of Mathematics, Strasbourg, 18 November 2022) - recording by the author (in French, with English subtitles).
  • "Rhythmic Tiling Canons: theoretical aspects and compositional applications", invited talk at the Conservatory of Music of Trento, November 30, 2022 (slides and OM patches).
  • "“Prima la musica!” Some thoughts on Iannis Xenakis’ table of correspondences between the development of music and mathematics" (VIIth MusMat International Conference, Day 4, 21 October 2022) - Live streaming recording (39:30-1:01:30)
  • "The Music of Maths", keynote talk at the IMA Maths and Music Conference (London, Royal College of Music, 13-15 July 2022) - slides - some photos souvenirs
  • "An Interactive Tool for Composing (with) Automorphisms in the Colored Cube Dance" (joint paper co-authored with Alexandre Popoff and Corentin Guichaoua) presented at the Mathematics and Computation in Music Conference 2022 (Atlanta, USA, 21-24 June 2022) - slides and paper
  • "Music and Math: the reason of a match", invited conference-concert, Italy Sounds Classic, Bologna, June 9-11 2022 - slides.
  • "Mathématiques, dessinez-moi la musique", PAF, ENS-Lyon, May 19-20 2022 - slides. Talk on the LaLaLab Exhibition slides
  • Math'n Pop @ Kantor (Lyon, France, 19 Mai 2022)
  • Le Curieux Festival (Strasbourg, 18-23 April 2022). Link to the teaser The formula to write a hit (in French).
  • "Maths in music…the music of maths!", International Day of Mathematics (14 March 2022, online) - video recording (30:46-40:10).
  • "From music to maths and backwards: introducing algebra, topology and category theory into computational musicology" (Dpt of mathematics, University of Trento, 25 November 2021) - slides.
  • A special PhiloMaths&Song session at the mamuphi (mathematics, music & philosophy) seminar at IRCAM (Salle Stravinsky, Saturday, 13 November, 10am-6pm) - Schedule - videos (morning sessions) and videos (afternoon sessions).


NEWS

Structure of the project:

  • Initial financial support: USIAS - University of Strasbourg Institute for Advanced Studies (2017-2019)
  • Currently hosted by IRMA - Institut de Recherche Mathématique Avancée (UMR 7501), University of Strasbourg (in collaboration with IRCAM, STMS Lab of CNRS and the CREAA Interdisciplinary Institute). The SMIR Project also includes two new research directions:
    • Mathemusical Learning Processes. This investigation is carried on within the ProAppMaMu Project (=Processus et techniques d'apprentissages des savoirs 'mathémusicaux') supported by the MITI (Mission pour les initiatives transverses et interdisciplinaires) of CNRS.
    • Mathemusical Outreach. A series of large public actions on maths & music are conceived and carried on within the SMIR2C Project (=Structural Music Information Research 2 CITE) supported by the Université&Cité IDEX Program of the University of Strasbourg
  • Members of the research team:
    • Moreno Andreatta (Principal Investigator), CNRS Research Director at IRMA/University of Strasbourg, and associate researcher at the STMS Lab, Sorbonne University
    • Paul Lascabettes, post-doctoral fellow at the ITI IRMIA++ and CREAA/University of Strasbourg and associated researcher at the STMS Lab, Sorbonne University
    • Athanase Papadopoulos (Research Director at IRMA UMR 7501, Strasbourg)
    • Pierre Guillot (Assistant Professor in mathematics - UMR 7501 IRMA, Strasbourg)
    • Nicolas Juillet (Professor in mathematics - IRIMAS, University of Haute Alsace, Mulhouse)
    • Xavier Hascher (Professor in musicology - EA 3402 ACCRA, University of Strasbourg)
    • José-Luis Besada (post-doctoral researcher, Universidad Complutense de Madrid)
    • Corentin Guichaoua (researcher and main developer of the Tonnetz and Rhythm Circle web environments, LaMaMu project, CREAA/University of Strasbourg)
    • Erica Bisesi (post-doctoral researcher, Associate Professor at the University of Montréal)
    • Victoria Callet (ATER at the University of Strasbourg and responsible of the mathematics & music research program at IREM/University of Strasbourg
    • Matías Fernández Rosales (PhD student in composition, University of Strasbourg/HEAR-Conservatory of Strasbourg. Co-supervision with Xavier Hascher and Daniel D'Adamo)
    • Marie Marty (freelance designer)
  • Alumni:
    • Riccardo Gilblas (PhD student in mathematics, University of Padova/University of Strasburg, co-supervision with Luisa Fiorot). Thesis defended at the University of Padova, April 8, 2024 - manuscript
    • Maximilien Wang (Master 2 student in mathematics on persistent homology applied to music, University of Bordeaux, 2022-2023) - Dissertation
    • Raphaël Schnoering (Master 1 student in mathematics on homometric musical structures, University of Strasbourg, 2022-2023)
    • Mathieu Lefèvre (Master 1 student in computer science on musical data analysis and machine learning, University of Strasbourg, 2022-2023. Co-supervision with Stella Marc-Zwecker)
    • Greta Lanzarotto (PhD student in mathematics in cotutelle, University of Pavia/University of Strasbourg, co-supervision with Ludovico Pernazza). Thesis defended in 2021 - abstract - manuscript
    • Christophe Weis (Master 2 student, codirection with Isabelle Bloch, Télécom ParisTech, and Carlos Agon, Sorbonne University/Ircam/CNRS, 2021-2022) - Dissertation
    • Judith Gaetcher (Master 1 MEEF student, codirection with Grazia Giacco, University of Strasbourg, 2021-2022) - Dissertation
    • Térence Viaud (L3 student in mathematics, University of Orsay, 2021-2022) - vidéo
    • Guillaume Rousseau (Master 2 student in maths & computer science at the ENS of Lyon, 2020-2021) - pdf
    • Damien Di Napoli (Master 1 student in mathematics on Babbitt's Hexachord Theorem, University of Strasbourg, 2020-2021)
    • Manos Karistineos (Master 2 student in mathematics on mathematical morphology applied to music analysis, University Paris 7)
    • Paul Lanthier (PhD student in mathematics on cellular automata applied to music composition, University of Rouen)
    • Charlotte Vulliez (Master 1 student in mathematics, University of Strasbourg, 2018-2019)
    • Sonia Cannas (PhD student in mathematics, co-supervision with Ludovico Pernazza, University of Pavia and Athanase Papadopoulos, université de Strasbourg, cotutelle-agreement) - pdf
    • Paul Lascabettes (Master 1 student, ENS-Saclay, co-supervised with Corentin Guichaoua, 2017-2018 and Master 2 student, ATIAM, co-supervised with Carlos Agon and Isabelle Bloch, 2018-2019) - M1 Dissertation and M2 Dissertation
    • Matteo Pennesi (Master 2 student, codirection with Massimo Ferri, University of Bologna) - 2017-2018
    • Corentin Bayette (Master 1 student at the University of Strasbourg, co-supervised with Corentin Guichaoua) - 2017-2018 - Dissertation
    • Xavier Dambach (Master 2 student at the University of Strasbourg, supervised by Corentin Guichaoua) - 2017-2018
    • Grégoire Genuys (PhD student, codirection with Jean-Paul Allouche, UPMC) - Dissertation and thesis presentation
    • Pierre M. Relaño, mathematician and composer (composition and computer music classes by Daniel D’Adamo and Tom Mays, Conservatory of Strasbourg)
    • Killian Herraez (Master 2 student, codirection with Isabelle Bloch, Télécom ParisTech, Jamal Atif, université Paris Dauphine and Carlos Agon, UPMC/Ircam/CNRS) - Dissertation and master thesis presentation
  • Complete list of collaborators and field of interest:
    • Athanase Papadopoulos (Geometry and history of maths/music) - UMR 7501 IRMA, Strasbourg
    • Yann Bugeaud (Algebraic numbers and tilings) - UMR 7501 IRMA, Strasbourg
    • Alessandro Arbo (Musicology, musical aesthetics) - CREAA, Strasbourg
    • Xavier Hascher (Transformational music analysis) - CREAA, Strasbourg
    • Pierre Michel (Contemporary music and improvisation) - CREAA, Strasbourg
    • Nathalie Herold (Complex Systems & music, rhythm and form in XXth Century music) - IReMUS, Sorbonne University
    • Tom Mays (Composition and computer music) - GREAM/HEAR/Conservatory of Strasbourg
    • Daniel D’Adamo (Composition) - HEAR/Conservatory of Strasbourg
    • Georges Bloch (Computer-aided composition/improvisation) - University of Strasbourg / IRCAM
    • Olivia Caramello (Category and topos theory) - IHES, Bures-sur-Yvette, Paris-Saclay
    • Pierre Cartier (Category theory and music representations) - IHES, Bures-sur-Yvette, Paris-Saclay
    • Alain Connes (Spectral theory and music) - IHES, Bures-sur-Yvette, Paris-Saclay
    • Gérard Assayag (Computational musicology) - IRCAM/CNRS UMR 9912/Sorbonne University, Paris
    • Carlos Agon (Visual programming languages) - IRCAM/CNRS UMR 9912/Sorbonne University, Paris
    • Karim Haddad (computer-aided composition) - IRCAM/CNRS UMR 9912/Sorbonne University)
    • Andrea Agostini (Computer-aided analysis and composition) - IRCAM/CNRS UMR 9912/Sorbonne University, Paris
    • Daniele Ghisi (Computer-aided analysis and composition) - IRCAM/CNRS UMR 9912/Sorbonne University, Paris
    • Jean-Louis Giavitto (Programming languages and topology) - IRCAM/CNRS UMR 9912/Sorbonne University, Paris
    • Jean Bresson (Visual programming languages) - IRCAM/CNRS UMR 9912/Sorbonne University, Paris
    • Davide Stefani (Category theory (PhD student) - UPMC / ENS, Paris
    • Grégory Ginot (Persistent homology and category theory) - Sorbonne University, Paris
    • Jean-Paul Allouche (Combinatorics and number theory) - CNRS/Sorbonne University, Paris
    • Louis Bigo (Topology in computer-aided music analysis) - CRIStAL, University of Lille 3
    • Isabelle Bloch (Mathematical Morphology) - LTCI, Télécom ParisTech
    • Jamal Atif (Formal Concept Analysis / computer science) - LAMSADE / University of Paris-Dauphine
    • Polo (Pierre Lamy) - Song writing and composition
    • Ludovico Pernazza (Algebra and geometry) - University of Pavia
    • Sonia Cannas (Transformational theory, PhD student) - Univ. of Pavia /Univ. of Strasbourg
    • Massimo Ferri (Persistent homology) - University of Bologna
    • Elaine Chew (Mathemusical research and performance) - Queen Mary University of London
    • David Meredith (Symbolic music information retrieval) - Aalborg University
    • Thomas Noll (Mathematical Music Theory) - TU-Berlin / ESMuC Barcelona
    • Thomas Fiore (Category theory and music analysis) - University of Michigan-Dearborn, USA
    • Andrée Ehresmann (Category theory and cognitive sciences) - Université de Picardie
    • Alexandre Popoff (Category theory and Transformational Theory) - Paris
    • Emmanuel Amiot (Mathemusical research with focus on DFT) - Perpignan
    • Gilles Baroin (Mathemusical research and visualisation) - Toulouse
    • Alberto Tonolo (Professor in mathematics, University of Padova)
    • Luisa Fiorot (Associate Professor in mathematics, University of Padova)


Some useful conference presentations:

  • Alexandre Popoff has given a talk within the new IRMA-CREAA mathemusical seminar (Department of Mathematics, Strasbourg, 18 November 2022, 4pm)
  • Moreno Andreatta, Andréee Ehresmann, Alexandre Popoff, "Analyse musicale transformationnelle et théorie des catégories", mamuphi Seminar, ENS Paris, 7 February 2015 (pdf and video)
  • Moreno Andreatta, Andréee Ehresmann, Alexandre Popoff, "Théories des catégories en Analyse Musicale", SIC (Séminaire Itinérant des catégories), Lille, 23 March 2016 (pdf)
  • Andréee Ehresmann and Alexandre Popoff, "Andrée Ehresmann et Alexandre Popoff: "Approche Catégorielle en Analyse musicale", IRMA/USIAS Mathemusical Seminar, IRMA, Strasbourg, 23 February 2018 (pdf)


Visitors:


Past events:

(click to see Etienne Lécroart's animation done with bouboucle by Andréas Kündig and Ivan Gulizia)



logo-smir-project.jpg




(back to the main homepage at IRCAM and to the Maths & Popular Music Course)

 


moreno/smir.txt · Dernière modification: 2024/12/05 12:09 par Moreno Andreatta